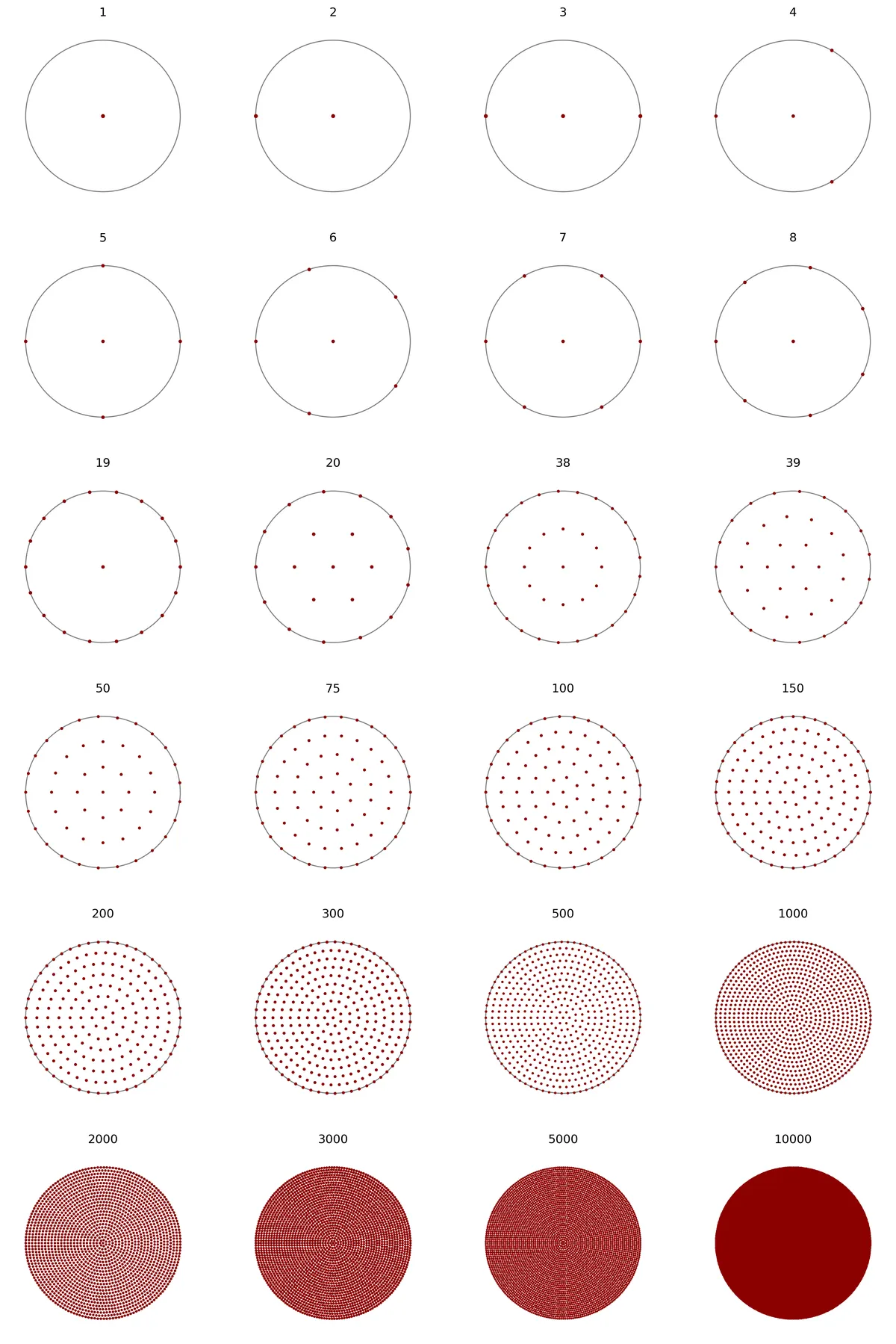
Non-random uniform disk sampling

27 Jan, 2025

Consider the problem of generating N points on a disk of diameter D. The function must be deterministic and the points somewhat uniformly spread around on the disk. Importantly, I want to generate exactly N points, for any integer value of N.

Here's what I mean with $N = 1721$ :

I needed to solve that problem recently, and this is what I came up with.

First, we know that the first point will be hardcoded at the origin (0,0) so it's safe to ignore it as we'll manually add it anyway, and consider only N-1 points for the next part.

Let's define an integer M. We will spread our N-1 remaining points over M concentric rings. Let $S_{i}$ be the number of points on ring $i$ . We want:

\sum S_{i} = N - 1

How should the number of points vary from ring to ring? Well, if rings are linearly spaced from the center, their radiuses are a linear progression, so it seems a good idea to have the number of points per ring be proportional to the ring perimeter. Let's call that proportion $α$ :

S_{i} = 2 π R_{i} α

We choose uniform concentric rings, aka $R_{i} = [1, 2, \dots, M]$ , so:

2 π α \sum R_{i} = N - 1

We know that $\sum R_{i} = \frac{M (M + 1)}{2}$ , so:

α = \frac{N - 1}{π M (M + 1)}

This gives a good value for $α$ , but there is still the issue of choosing a value for M.

Let's look at what values are possible for $M$ . Using the reasonable constraint that we want $α > 1$ this gives this quadratic inequality for choosing $M$ :

π M^{2} + π M + (1 - N) < 0

This quadratic polynomial will be negative when $M$ is between its roots. And since we obviously want a positive number of rings, this gives us bounds for $M$ . Let's looks at the roots of this polynomial for integer values between 1 and 20:

 N     M1     M2
 1   0.25  -1.25
 2   0.44  -1.44
 3   0.60  -1.60
 4   0.73  -1.73
 5   0.86  -1.86
 6   0.97  -1.97
 7   1.07  -2.07
 8   1.17  -2.17
 9   1.26  -2.26
10   1.35  -2.35
11   1.44  -2.44
12   1.52  -2.52
13   1.59  -2.59
14   1.67  -2.67
15   1.74  -2.74
16   1.81  -2.81
17   1.88  -2.88
18   1.95  -2.95
19   2.01  -3.01
20   2.07  -3.07

Not only does the positive root grow quite slow, we have to be careful of rounding. For the rest of this article, I'll choose the maximum value for $M$ , which gives maximum "density" of points, so to speak. But any value less than that is possible. Use a lower M value for a more "ringy" looking sampling, and the maximum value for most "dense" looking sampling.

So, here is the formula for maximum M value:

M_{m a x} = floor (\frac{- π + \sqrt{π^{2} - 4 π (1 - N)}}{2 π})

Now that we have $M$ and $α$ , getting $S_{i}$ is easy from the formula above! Here's what we get for N=50:

import numpy as np

N = 50
M = np.floor((-np.pi + math.sqrt(np.pi**2 - 4*np.pi*(1-N))) / (2*np.pi))
alpha = (N-1)/(math.pi*M*(M+1))
R = np.arange(1, M+1)
S = 2*np.pi*alpha*R

print(S)
print("sum = ", S.sum())

[ 8.16666667 16.33333333 24.5       ]
sum =  49.0

Yes! We got it! That's our number of points per ring, and the sum is a perfect $N - 1 = 49$ ! With the additional center point, that's the 50 we want!

But wait! Those are real numbers... we need an integer number of points per ring. How do we go from $S_{i}$ to an array of integers?

Well, there's probably a lot of ways to accomplish that. For me, I choose a simple trick. First, round S and check the sum again. With some luck, that sum is still $N - 1$ . If not, subtract the difference from the last element of $S_{i}$ . This is quick and easy, and the last ring is the one with the most points, making this choice hardly noticeable.

Converting the number of points per ring to actual point coordinates is then just a matter of sampling in polar coordinates and converting to Cartesian. This is the full uniform_disk_sampling() function in Python:

import numpy as np

def uniform_disk_sampling(N, diameter):
    M = np.floor((-np.pi + np.sqrt(np.pi**2 - 4*np.pi*(1-N))) / (2*np.pi))
    if M == 0:
        M = 1
    alpha = (N-1)/(np.pi*M*(M+1))
    R = np.arange(1, M+1)
    S = 2*np.pi*alpha*R

    # If we're off, subtract the difference from the last element
    S = np.round(S)
    S[-1] -= (S.sum() - (N - 1))
    S = S.astype(int)

    # List of sample points, start with the origin point
    points = [np.zeros((1, 2))]

    for s, r in zip(S, R):
        theta = np.linspace(-np.pi, np.pi, s+1)[:-1]
        radius = r/M * diameter/2
        points.append(np.column_stack((radius*np.cos(theta), radius*np.sin(theta))))

    return np.vstack(points)

And this is what it looks like from N=1 to 10000:

post4img4